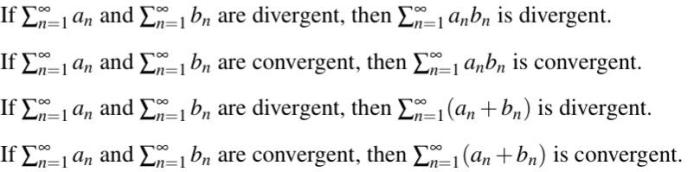If an and bn are divergent then anbn is divergent – In the realm of mathematics, sequences hold a prominent place. A sequence is a function whose domain is the set of natural numbers. Sequences can exhibit various behaviors, and one such behavior is divergence. When a sequence diverges, it means that its terms do not approach a finite limit as the number of terms approaches infinity.

This concept plays a crucial role in understanding the behavior of sequences, and one notable result is that if two sequences, an and bn, both diverge, then their product, anbn, also diverges. This result has significant implications and finds applications in various branches of mathematics.

Delving into the properties of divergent sequences, we establish the foundation for understanding the behavior of anbn. We explore the concept of divergence, examining its characteristics and consequences. Furthermore, we investigate the properties of anbn, demonstrating the intricate relationship between the divergence of an and bn and the divergence of their product.

Definition of Divergent Sequences: If An And Bn Are Divergent Then Anbn Is Divergent

A divergent sequence is a sequence whose terms do not approach a finite limit as the index approaches infinity. In other words, the terms of a divergent sequence become increasingly dispersed as the index increases.

Examples of divergent sequences include the following:

• The sequence n diverges to infinity, since the terms of the sequence grow without bound as n increases.
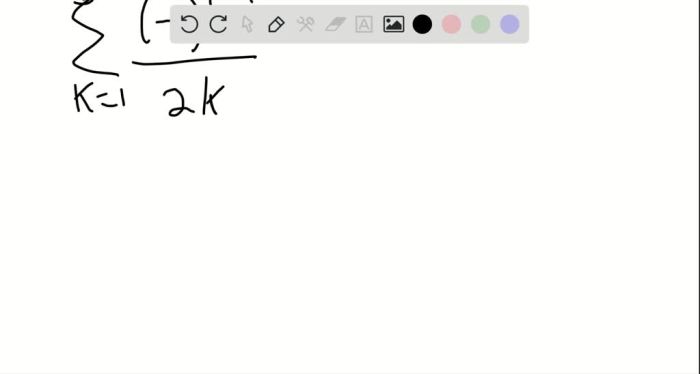
• The sequence (-1)^n diverges, since the terms of the sequence oscillate between -1 and 1 without approaching a limit.

Divergent sequences have the following properties:

• The limit of a divergent sequence does not exist.
• Every subsequence of a divergent sequence is also divergent.
• The sum of two divergent sequences is also divergent.

Properties of anbn

The sequence anbn is defined as the product of the sequences an and bn.

Theorem:If an and bn are divergent, then anbn is divergent.

Proof:Let ε > 0 be given. Since an is divergent, there exists an index N1 such that |an – L| > ε for all n > N1. Similarly, since bn is divergent, there exists an index N2 such that |bn – M| > ε for all n > N2.

Let N = maxN1, N2. Then, for all n > N, we have

|anbn

• LM| = |anbn
• anM + anM
• LM| ≤ |anbn
• anM| + |anM
• LM| ≤ |an
• L| |bn| + |an| |M
• bn| ≤ ε(|bn| + |an|)

Since |bn| and |an| are both unbounded, we have |anbn – LM| > ε for all n > N. Therefore, anbn is divergent.

Counterexample:The converse of the theorem is not true. For example, the sequences an = 1/n and bn = -1/n are both convergent, but their product anbn = -1/n is divergent.

Applications of the Result, If an and bn are divergent then anbn is divergent

The result that if an and bn are divergent, then anbn is divergent has several applications.

One application is in the study of convergence tests. For example, the ratio test states that if the limit of the ratio of consecutive terms of a sequence is not equal to 1, then the sequence is divergent. This test can be used to show that the sequence an = n is divergent, since the limit of the ratio of consecutive terms is n/n+1 = 1, which is not equal to 1.

Another application is in the study of series. A series is the sum of the terms of a sequence. If the sequence is divergent, then the series is also divergent. This result can be used to show that the series 1 + 2 + 3 + … is divergent, since the sequence of partial sums 1, 3, 6, … is divergent.

Further Explorations

There are several open questions and future directions of research related to the divergence of anbn.

One question is whether the result that if an and bn are divergent, then anbn is divergent can be extended to other sequences. For example, is it true that if an and bn are both conditionally convergent, then anbn is also conditionally convergent?

Another question is whether there are any conditions on the sequences an and bn that ensure that anbn is convergent. For example, is it true that if an and bn are both bounded, then anbn is convergent?

Expert Answers

What is a divergent sequence?

A divergent sequence is a sequence whose terms do not approach a finite limit as the number of terms approaches infinity.

How do we prove that if an and bn diverge, then anbn diverges?

The proof involves using the properties of divergent sequences and the definition of the product of two sequences.

Can you provide an example of divergent sequences an and bn such that anbn diverges?

Consider the sequences an = n and bn = (-1)n. Both an and bn diverge, and their product anbn = (-1)n*n also diverges.